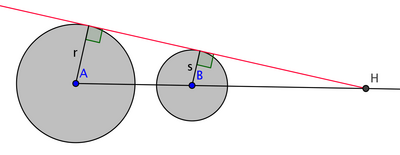
So JD asked if we could construct a tangent to two circles. I knew I'd seen it done, but I'm pretty sure what I came up with isn't the method I'd seen. It's not too bad, though.

The idea is simple: in the sketch, you can see that we have similar right triangles once the tangent is in place, and so AH:BH=r:s. Thus, I need BH(r-s)=s.AB, which I can construct easily enough.
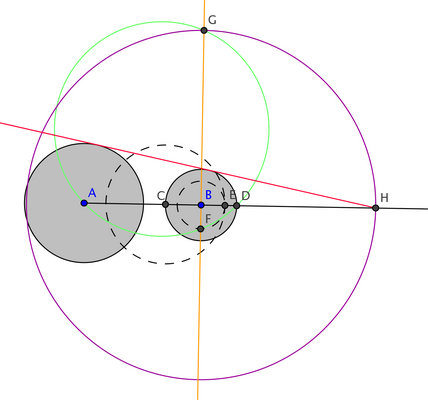
Let the smaller circle centred B intersect the (black) line of centres at C, D. Make another circle radius r centred on C, giving point E. Pick a point F on circle centre B through E. Now construct the green circle ADF and put G where it intersects the orange line FB. The intersecting chord theorem tells me that AB.DB=BF.BG, so since BF=r-s I have the length I wanted. H, then, is the point to construct my tangent from, and from here it's well known.
UPDATE: Another poster reminded me of the more elegant method, which is well worth putting here. We draw any line through A not through B (here in green), and the parallel line through B:
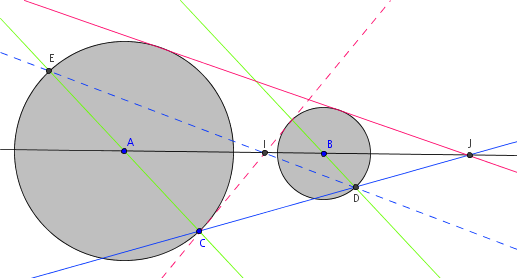
Now the line CD gives ACJ, ADJ similar triangles in the ratios we wanted, so J is the proper point to base our (red) tangent line from! This is obviously far quicker than my method; I tend to be bad at thinking of methods that start with "draw any other line", for some reason.
You also get the interior tangents "for free", shown dotted, by a very similar method.
UPDATE 2: And JD tells us this, beautiful, method (my own explanation):
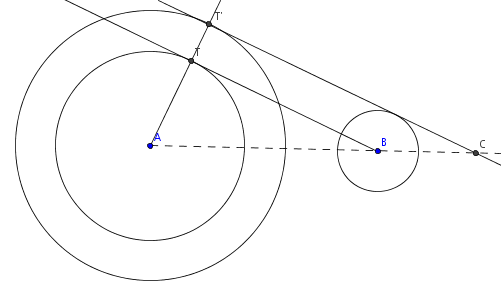
Consider the diagram. Again the big circle about A has radius r, the circle about on B has radius s. Now BC:s = AC:r = AB:r-s. So construct by a method of your choice (such as I used in my own method, say) the circle about A with radius r-s, and the tangent TB drawn. Then the tangent T'C we want is parallel; so extend AT to T' and draw in the perpendicular. We don't even need the line AB or the point C except to explain it. Beautiful.